[la fibre technique #14]
Les choses ne tiennent parfois qu’à un fil.

Les choses ne tiennent parfois qu’à un fil. En câblerie elles tiennent toujours à plusieurs. Encore faut-il que chacun trouve la meilleure place dans les gaines 😉

Je vous explique ?

Concevoir un #câble à fibres optiques idéal n’est pas aussi simple qu’un coup de fil. Si sur le terrain rien ne ressemble plus à un câble qu’un autre câble, les différentes rigidités, les différentes matières, les différentes fonctions des produits imposent l’utilisation de calculs de simulation et de modélisation. Et avant que cet ensemble d’éléments cylindriques ou tubulaires assemblés entre eux supporte le transport d’informations à près de 200 000 km/s, quelques règles s’imposent.

👉 Première règle à ne jamais oublier, une #fibre optique est composée de verre et de résines acrylates. Elle est donc mécaniquement peu sensible aux effets de la température dans les plages normales d’utilisation (-40 +70°C). Ses caractéristiques de dilatation sont négligeables et elle ne présente pas de post retrait, relativement aux matériaux plastiques qui l’entourent.

👉 Ensuite, quand elles sont libres -en micromodule ou loose tube- les fibres prennent une forme hélicoïdale, et leur longueur dans le module est de fait supérieure à la longueur du module lui-même.

👉 Quant au diamètre intérieur du module, il est plus grand que le diamètre circonscrit à l’ensemble des fibres. Fibres dont il faut considérer qu’elles ondulent dans le module, au gré des signaux qui les traversent.

Voilà à quoi servent les calculs ➡️ déterminer le diamètre optimal d’un module via la détermination de ce diamètre circonscrit.

Plusieurs méthodes de calculs existent mais la surfacique corrigée est celle que j’utilise le plus car elle donne des résultats relativement précis, surtout pour des éléments de petites dimensions.

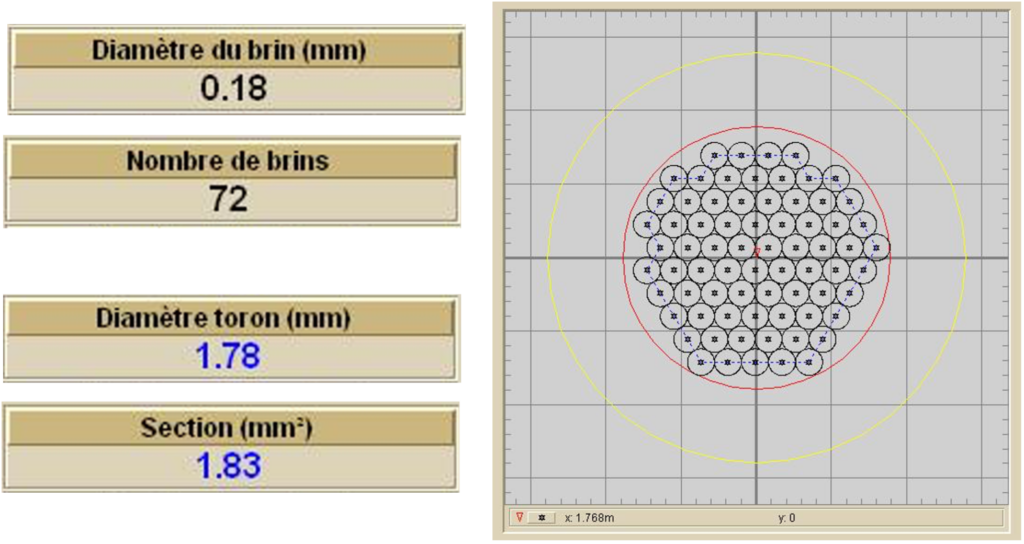
💡Cette méthode consiste à additionner l’ensemble des sections de fibres du module pour en déterminer le diamètre équivalent. Par exemple, pour un module de 12 fibres de 250 µm de diamètre (df), le diamètre apparent (Da) sera Da = df x √ (12). A partir de Da, le diamètre circonscrit (Dc) à l’ensemble des 12 fibres est calculé en intégrant « les petits espaces vides entre les fibres ». Imaginons empiriquement que ces espaces vacants représentent 30% de la section totale contenue à l’intérieur de DC. Alors le diamètre circonscrit est obtenu en insérant un facteur 0,7 au dénominateur sous la racine, soit Dc = df x √ (12/0,7).

Les outils de simulation numérique actuels autorisent des calculs très précis concernant les dimensionnels. Ils sont donc des alliés de poids en ces heures de grande miniaturisation.
J’aurais plaisir à vous les faire découvrir dans mon prochain post, avec un exemple détaillé.