[la fibre technique #1]
Bandes de transmission et atténuation

Comme souvent dans l’histoire des sciences, l’optique n’a pas échappé au débat. Débat qui s’est étendu sur près de 400 ans, avec Huygens ou Newton qui s’opposaient sur la nature même de la lumière. Il faut attendre 1909 pour qu’Einstein fasse converger leurs deux points de vue et pose le principe de la dualité onde-corpuscule, qui permet de considérer la lumière comme :

〰 une onde d’où la notion de longueur d’onde
☀ et comme un flot de corpuscules appelés photons.

Ces deux théories ne se contredisent pas, elles se complètent. L’une ou l’autre permettent juste d’expliquer les phénomènes physiques de propagation dans une fibre.

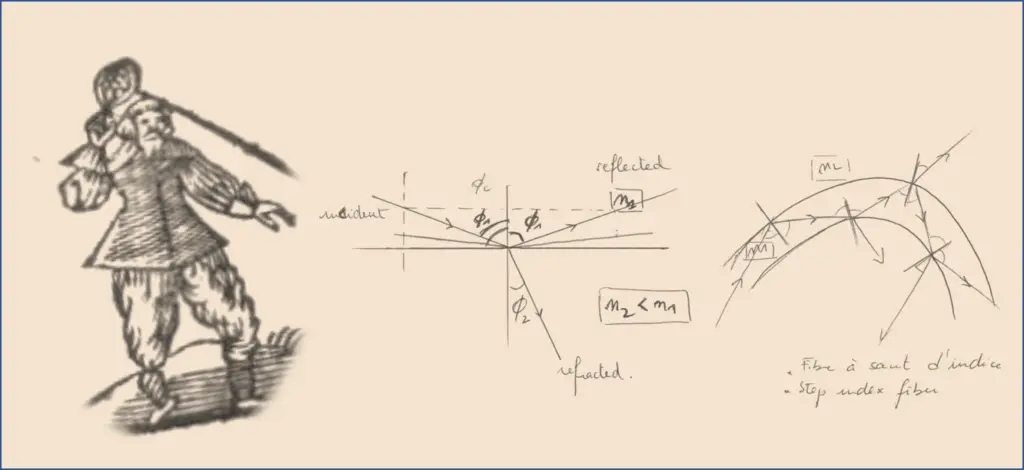
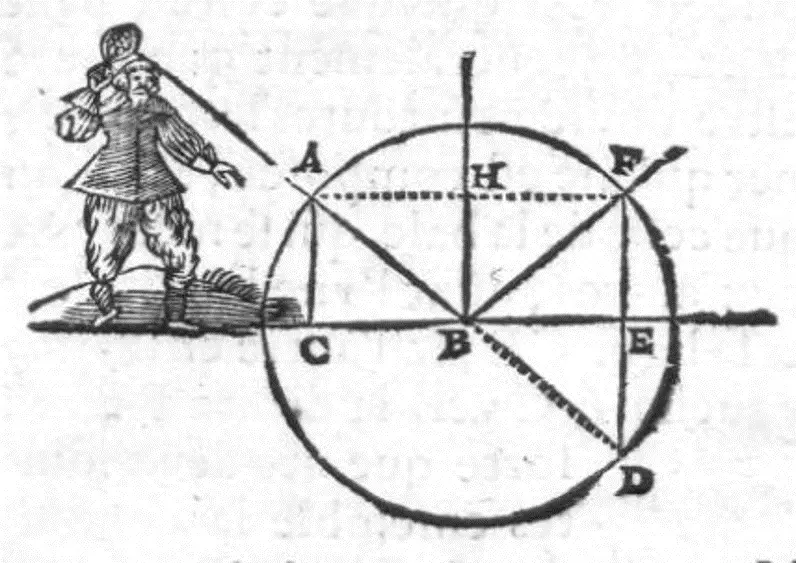
〰 Dans la première théorie, la lumière est vue comme un ensemble de photons constituant un rayon lumineux, qui se propage, et suit un chemin qui minimise son temps de parcours. De ce principe découle l’optique géométrique (Principe de Fermat 1657), ainsi que les lois de Snell-Descartes (un double-nom pour solder une querelle de priorité âprement débattue 😮‍💨).

🔬 La première loi exprime le comportement d’un rayon lumineux lorsqu’il se réfléchit sur une surface (ex. une balle sur du béton).

🔬🔬 La seconde exprime le changement de direction d’un faisceau lumineux lors de la traversée d’une paroi séparant deux milieux différents (ex. un rayon du soleil pénétrant dans la mer).

Le rayon lumineux est alors dit incident avant d’avoir rencontré la surface, il est dit réfléchi ou réfracté après.

Une fois précisé que :
👉 l’indice du milieu ni est le rapport de la vitesse de la lumière dans le vide (c) sur la vitesse de la lumière dans le milieu considéré (vi), soit ni = c / vi
👉 et considérant un rayon incident avec un angle Ø1 par rapport à une perpendiculaire de la frontière des deux milieux respectivement d’indice n1 et n2, où n1 est l’indice de réfraction du milieu dans lequel se propage le rayon incident, n2 celui du milieu dans lequel se propage le rayon réfracté, et avec n1 > n2, alors :

🔬 le rayon dans le milieu 1 se réfléchit sur l’interface avec le même angle Ø1.

🔬🔬 le rayon lumineux réfracté dans le milieu 2 suit un chemin avec un angle Ø2 qui obéit à la loi [ n1 * sin(Ø1) = n2 * sin(Ø2) ]

Cas particulier : il existe un angle Øc pour lequel la réflexion est totale -pas d’onde réfractée- et qui obéit à la loi [ sin(Øc)= n2 / n1 ].

🌈 Le parcours de la lumière dans une fibre optique monomode à saut d’indice répond à ces principes. Idéalement elle se propage par réflexion multiple avec un angle qui est supérieur à l’angle Øc.

Mais dès lors que l’on courbe la fibre, l’angle de réflexion à l’endroit de la courbure change, devient inférieur à Øc et génère un rayon diffracté dans la gaine optique, synonyme de pertes optiques ou d’atténuation. Plus le rayon de courbure est faible, plus grande sera la perte optique du fait du nombre de réflexions qui augmente.

🔜 Dans le prochain épisode : Pertes par courbures et micro-courbures. Suivez le fil 🧵